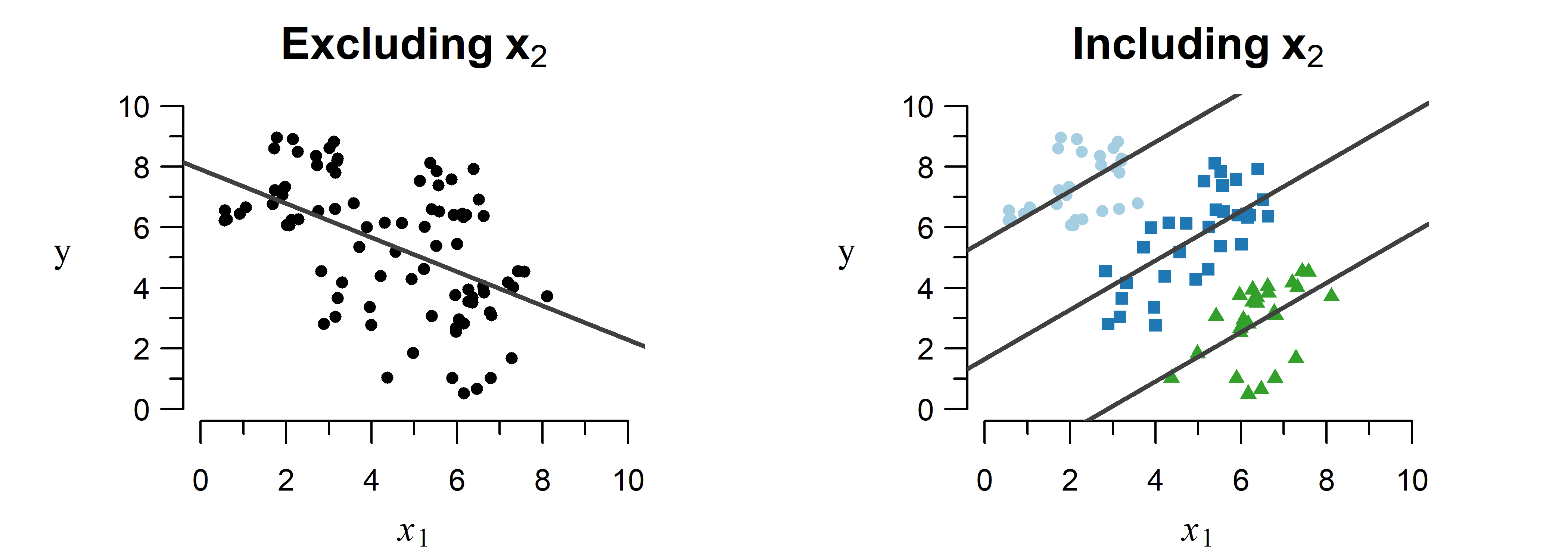3  Multiple Linear Regression

Linear regression with any number of explanatory variables.

Multiple linear regression allows you to simultaneously take into account the effect of multiple explanatory variables.

Why not just several one-on-one analyses?

One-on-one measures of association, like a correlation coefficient, are easy to compute and hence often used to explore relationships. However, these fail to reflect the complexity of real-life phenomena. Cancer is not caused by a single mutation; speciation not triggered by a single trait change.

Correlation analysis has been criticized in many biological fields, including clinical science [1]–[3], ecology [4] and evolutionary biology [5]. Key phenomena invalidating one-on-one analyses are explained below.

Estimating the effect of one variable without accounting for the effect of others can lead to a biased result.

Figure 3.1: True causal relationship (left) and biased estimate (right) if \(\boldsymbol{O}\) is not included in the analysis.

In a study on asbestos exposure, smoking may be more common among individuals exposed to asbestos. This would lead to an overestimated effect of asbestos, if smoking behavior is not adjusted for. Large systematic reviews on asbestos exposure therefore almost always adjust for smoking [6]–[8].

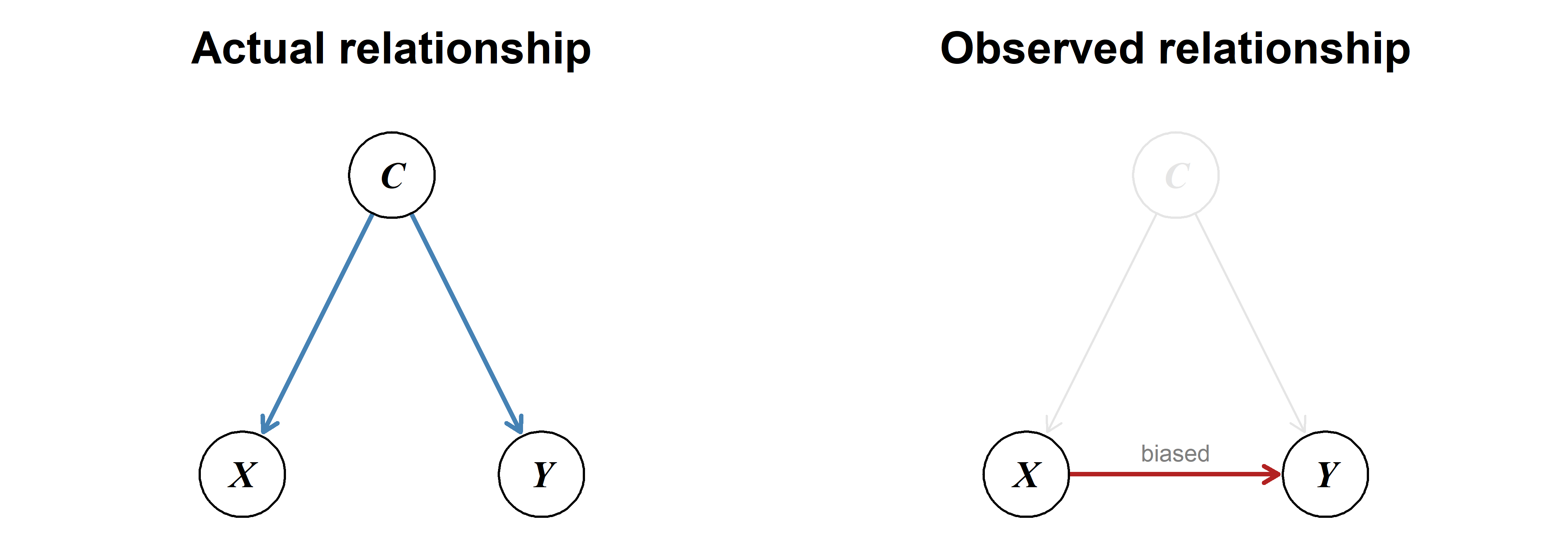
A special case of omitted-variable bias—unrelated variables can be correlated due to a third, unobserved variable.

Figure 3.2: True causal relationship (left) and biased estimate (right) if \(\boldsymbol{C}\) is not included in the analysis.

Coffee consumption is often linked to lung cancer, but this is caused by the confounding variable smoking: On average, smokers drink more coffee and are much more likely to develop lung cancer. Large overarching meta-analyses adjusting for smoking typically show that coffee consumption is not a risk factor for lung cancer [9]–[11].

Trends can appear, disappear and even completely change direction when including another variable in the model.

Figure 3.3: Observed trend excluding (left) and including (right) a grouping variable (\(x_2\)).

A study on kidney stones compared two methods for removal: open surgery and percutaneous nephrolithotomy (PN) [12]. Surprisingly, the less invasive PN method displayed a higher success rate than open surgery.

As shown in Table 3.1, this is an example of Simpson’s paradox: Separating by kidney stone size reveals that open surgery outperforms PN for both situations individually, but not when comparing the totals.

Table 3.1: Success rates of kidney stone removal methods by size.
Size Open Surgery Percutaneous
Nephrolithotomy
\(< 2\) cm \(\frac{81}{87}\) (93.1%) \(\frac{234}{270}\) (86.7%)
\(\geq 2\) cm \(\frac{192}{263}\) (73.0%) \(\frac{55}{80}\) (68.8%)
total \(\frac{273}{350}\) (78.0%) \(\frac{289}{350}\) (82.6%)

How is this contradiction possible? Open surgery is used in more often in severe cases (i.e., larger stones), which have a lower success rate. This lowers the total success rate below that of PN. Failing to account for this second variable (size) leads to the wrong conclusion that open surgery performs worse.

Contrary to one-on-one analyses, multiple regression can simultaneously take into account the effect of multiple contributing factors. This allows you to see what the effect of one variable is given the effect of all other included variables, which avoids the phenomena described above.